By: Luke Benz
April 6, 2018
This week’s FiveThirtyEight Riddler inquired about the number of “Transitive National Champions” in college basketball. Given that Villanova won the NCAA championship, we might first define a transitive national champion as any team the defeated Villanova during the 2017-18 season. But then, fans of teams who defeated the four transitive national champions (St. John’s, Butler, Providence, and Creighton) might proclaim their own teams deserving of a transitive championship. Thus, a transitive national champion is any team that either defeated Villanova or defeated another transitive national champion.
A quick piece of code shows that all 351 Division 1 are transitive national champions! This is pretty cool, and was certainly surprising to me. Perhaps a more interesting way to show that all 351 teams are transitive national champions is via a directed graph. That is, we draw an edge from team A to team B if team A defeated team B (Note since this a directed graph, A –> B is different than B–> A). Then, we can show that the resulting graph is connected, meaning there is a path from any vertex in the graph to any other vertex in the graph. Thus, every team is a transitive national champion because there is a path from every team to Villanova (denoted by the navy vertex). Showing that the graph is connected is actually an even stronger statement than showing all 351 teams are transitive national champions, as it demonstrates that all 351 teams would be transitive national champions regardless of who actually won the NCAA tournament.
If all 351 teams are transitive national champions, surely they can’t all be considered equally, right? We can examine the degrees of separation for each team to the national championship by examining the shortest chain possible to show that a team is a transitive national champion. In the graph representation above, this can be computed by finding the shortest path from any given team to Villanova. Only 23 teams are fewer than 3 degrees of separation from Villanova.
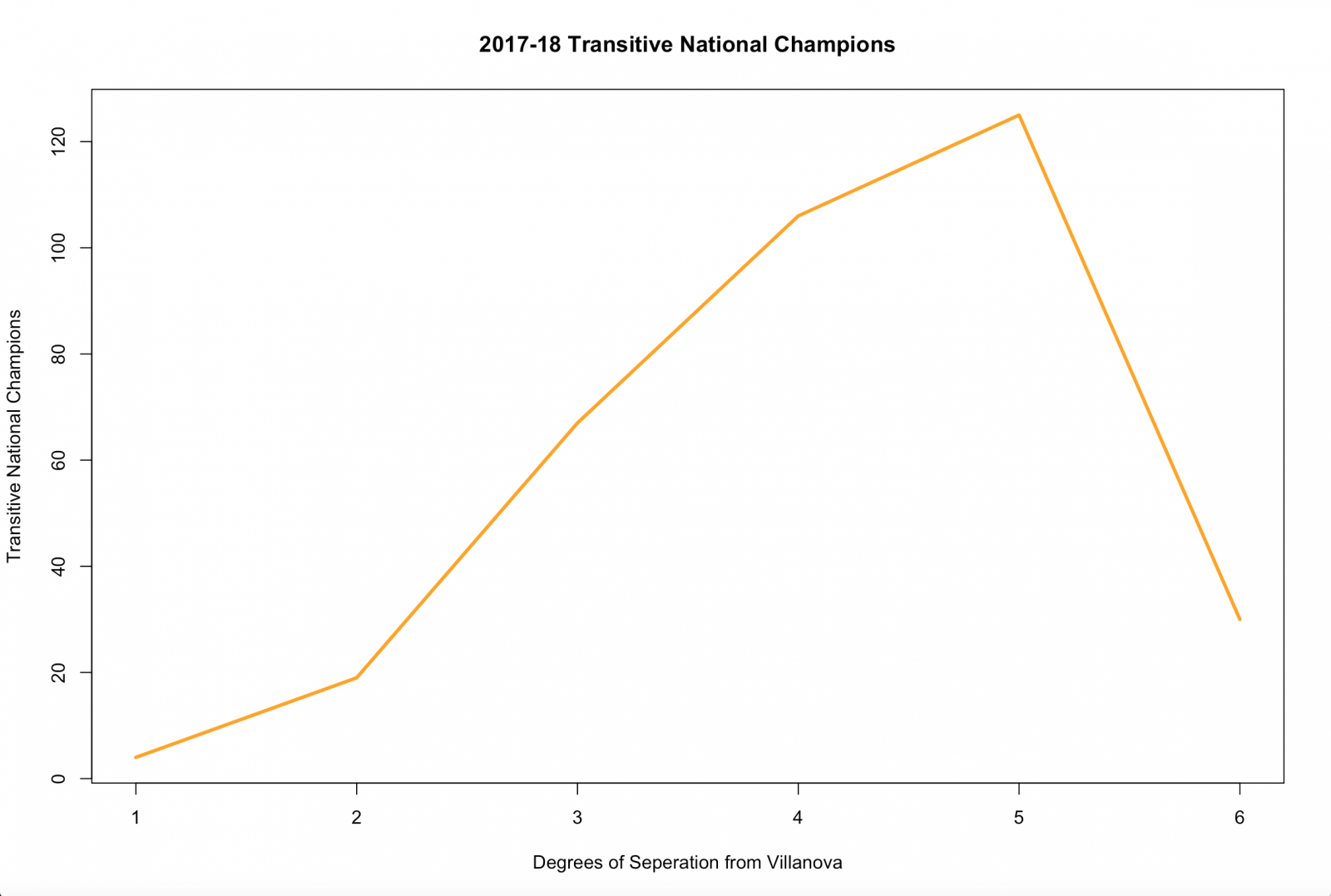
If you’d like to see the code used for this project, you can find it here.